Perceptive Locomotion on Unstructured Terrain
, , 2025
Summary
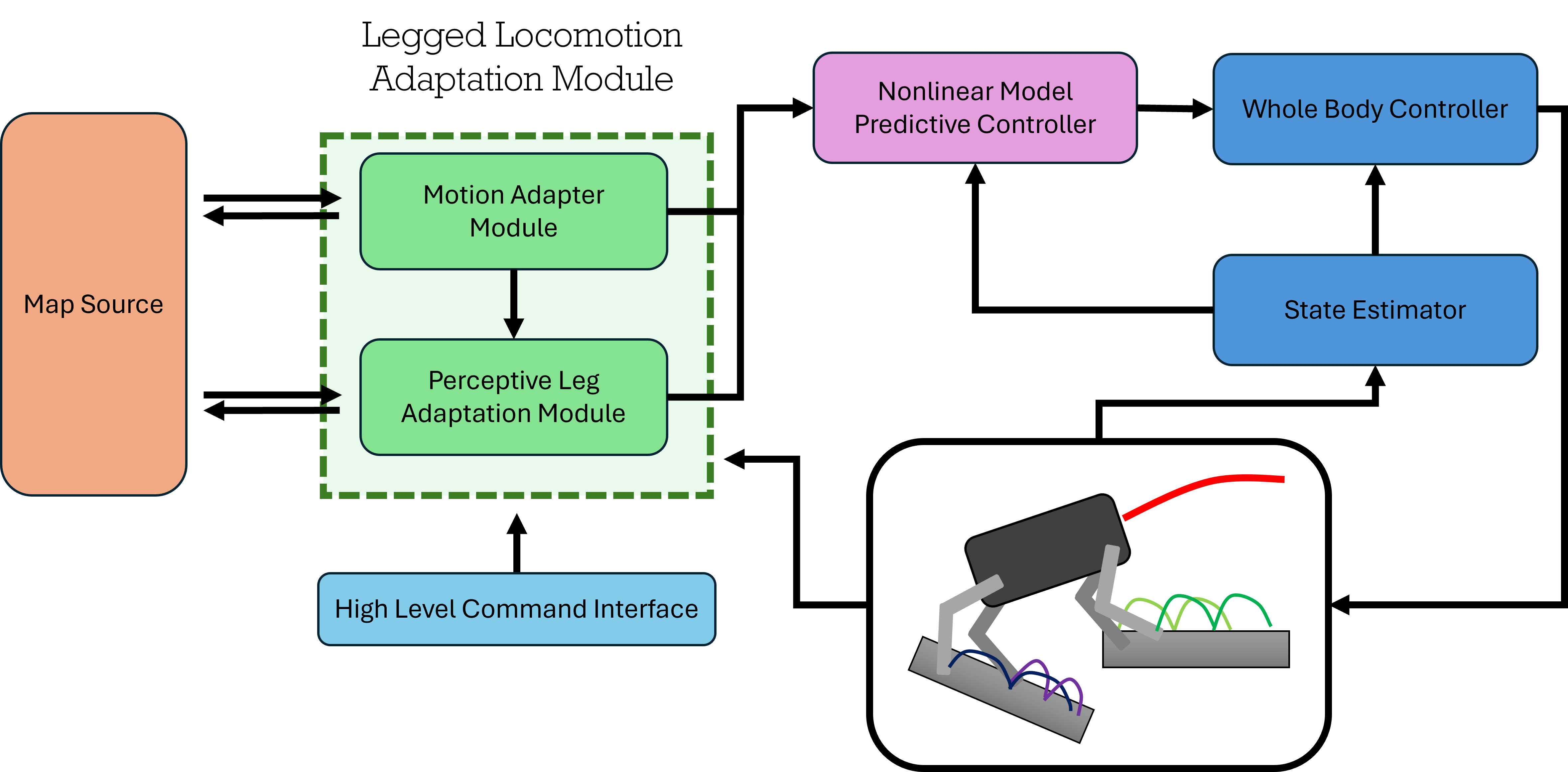
As shown in Figure 1, this work utilizes a Legged Locomotion Adaptation Module to modify reference trajectories for legged locomotion on uneven terrain. By utilizing map information that describes the geometry, edge, and traversability of the environment and a high level motion command, this work categorizes the locomotion problem into two motion trajectories that are to be transformed:
- The center of mass trajectory for generic motion planning of a single rigid body over rough terrains
- Foothold / Swing Trajectory of the leg over rough terrains
These trajectories are then used in the model predictive controller to find locally optimal solutions under dynamic system constraints. The following optimal control solution is then executed onto the robot, giving the next state, and thus, reiterates the method in real-time.
As a result, the methodology of adapting the trajectory to be locally optimized in the nonlinear model predictive controller (NMPC) works adequately well for the quadruped to walk over terrains such as ramps, stairs, pits, etc. Results can be seen in the subsection below, along with a case of failure.
Simulation Results
Simulation results of quadruped in a environment with potholes of 10cm in depth, stair environments with gap of 5cm, and a parkour course.
Hardware Results
Hardware results w/ static walking gait for stairs of 6-12cm in height and 25cm in depth and an environment with stepping stones.
Failure Cases
Hardware results w/ trot gait for stairs of 6-12cm in height and 25cm in depth.
General Architecture Overview
To understand briefly how the general architecture works, I will explain in more details about different components. More specifically, details about the the input sources and the Legged Locomotion Adaptaion Module will be expanded on while the controller and estimator will be briefly highlighted.
Input Sources
It is best look at the framework from Figure 1 starting from the input sources. The input starts with a general high-level motion trajectory. This can be in the form of a teleoperator control giving velocity commands to the robot, a target pose, or a high-level planner (e.g. A*, RRT-KD, etc.). Note, these high-level motion trajectories need not to be a fixed trajectory.
Independently of this motion trajectory, there also exists the input source in the form of the environment the robot is occupying. A 2.5D discretized elevation map is constructed from the environment by utilizing the grid map package, where filters such as in-painting, denoising, and edge detection are readily availble. Therefore, to form a environmental traversability metric, we construct a layer in the grid map $T_{env}(\mathbf{p}) \in [0, 1]$, where $\mathbf{p} \in \mathbb{R}^2$ is the position in the transverse plane, to signify how traversable different position within the environment is:
\[T_{env}(\mathbf{p}) = w_1(h - \bar h) + w_2(s(h)) + w_3\sigma(h),\]where $w_1 + w_2 + w_3 = 1$ are the weights, $(h - \bar h)$ is the roughness defined by the difference between the height and the smooth height, $s(h)$ is the slope defined as the projection of the normal vector along gravity, and $\sigma$ is the edge cost defined by a edge detection kernel.
Legged Locomotion Adaptation Module
The Legged Locomotion Adaptation module, shown in Figure 1, utilizes the high level command interface and the map to transform the trajectories for single rigid body locomotion to one such that there is some awareness of the terrain. These are decomposed into two components, the motion adapter module and the perceptive leg adaptation module, which will be explained in more detail in the two subsections.
Motion Adapter
The motion adapter in this work extends the legged_planner repository to a motion adapter utilizing environmental information. The initial repository utilizes an abstract class to interface different commands for motion planning and a motion adapter as a filter to transform the input trajectories into ones suitable for a legged robot. Thus, to extend the work to perceptive motion planning, we adjust the height of the floating rigid body corresponding to the height of the environment and align the orientation of the robot such that floating body is aligned with the terrain. These adapted trajectories are then used as reference for the nonlinear model predictive controller.
Perceptive Leg Adaptation Module
Correspondingly, the perceptive leg adaptation module tries to address the following maximization problem for traversability $T(\mathbf{x})$:
\[\max_{\mathbf{p}_i} T(\mathbf{x}) \\ s.t. \\ h_{foot,i}(\mathbf{x}) = h_{surface}(\mathbf{p}), \\ T(\mathbf{x}) \geq 0,\]where $\mathbf{p_i}$ are the foothold location for the $i$th leg, $T(\mathbf{x})$ is the traversability metric defined over the states of the legged robot $\mathbf{x}$, $h_{foot,i} = h_{surface}(\mathbf{p})$ ensures that the foot of the quadruped lies on the surface of the environment, and $T(\mathbf{x}) \geq 0$ is ensuring that the solution is over a traversability threshold.
There are have been various works that have address this in some form and various degrees (e.g. [1]-[3]), but this work looks to take a simplistic approach by first finding a nominal foothold, similar to [4]. Then, a locally optimal traversability foothold is selected by using a search based method around the nominal, locally maximizing the following traversability metric:
\[T(\mathbf{x}) = T_{env}(\mathbf{p}) + J_{default config}(\mathbf{x}),\]where $J_{default config}$ is a cost that helps select footholds close to the default joint configuration. Note, better cost can be utilize that gives more stability notions, but default joint configuration is adequate enough.
Once a foothold that is aware of the environment has been selected, these footholds are then utilized to form trajectories through hermite splines. These feet trajectories are then utilized as contraints in the nonlinear model predictive controller.
State Estimation
In perceptive locomotion, where having good localization data is important for understanding where the robot is within the environment, this work utilizes a motion capture system to get accurate localization data. This helps in the generating accurate footholds from the Perceptive Leg Adaptation Module with respect to the environment.
Note, however, we do interface the motion capture system with a two staged Kalman filter described in [4]. This allows us to utilize the Perceptive Leg Adaptation Module with and without the motion capture system. However, due to the drift in estimation, the Perceptive Leg Adaptation Module starts selecting footholds that do not meet traversability constraints and/or wrong footholds that are not on the surface of the environment. Therefore, we utilize the motion capture system to get ground truth localization to accurately select footholds.
Control
The control problem heavily relies on the ocs2 repository and the legged_control repository, that handles optimial control formulation for switched systems. As stated in the subsection Perceptive Leg Adaptation Module, the adapted reference trajectories are used as either reference trajectories, or constraints to the control formulation.
References
[1] F. Jenelten, T. Miki, A. E. Vijayan, M. Bjelonic and M. Hutter, “Perceptive Locomotion in Rough Terrain – Online Foothold Optimization,” in IEEE Robotics and Automation Letters, vol. 5, no. 4, pp. 5370-5376, Oct. 2020, doi: 10.1109/LRA.2020.3007427
[2] R. Grandia, F. Jenelten, S. Yang, F. Farshidian, and M. Hutter, “Perceptive Locomotion through Nonlinear Model Predictive Control,” (submitted to) IEEE Trans. Robot., no. August, 2022, doi: 10.48550/arXiv.2208.08373
[3] F. Jenelten, R. Grandia, F. Farshidian and M. Hutter, “TAMOLS: Terrain-Aware Motion Optimization for Legged Systems,” in IEEE Transactions on Robotics, vol. 38, no. 6, pp. 3395-3413, Dec. 2022, doi: 10.1109/TRO.2022.3186804.
[4] G. Bledt, M. J. Powell, B. Katz, J. Di Carlo, P. M. Wensing and S. Kim, “MIT Cheetah 3: Design and Control of a Robust, Dynamic Quadruped Robot,” 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 2018, pp. 2245-2252, doi: 10.1109/IROS.2018.8593885.
