Physics Informed Neural Network for Quadruped Dynamics
, , 2025
Introduction
Quadruped leg dynamics are hybrid, nonlinear, and high dimensional, causing many current approaches to model quadruped dynamics through methods such as linearization or approximated models. This causes many traditional locomotion of legged robots to consist of using hierarchal control where a high level planner generates a feasible center of mass trajectory for a simplified model and a lower level controller generates a trajectory of torque for a higher fidelity model. In this work, I attempt to use encoder and decoder neural networks with the Koopman operator theory as a means to deal with the nonlinear high dimensional hybrid leg dynamics of quadruped. This work focuses on modeling quadruped leg dynamics using the Koopman operator (i.e. capturing leg dynamics linearly in the lifted space) in hopes to use the rich history of linear control on quadruped without the need for a hierarchal controller in the future.
Click here to access the repository.
Brief Overview
Consider a nonlinear dynamical system
$x_{k+1} = f(x_k)$
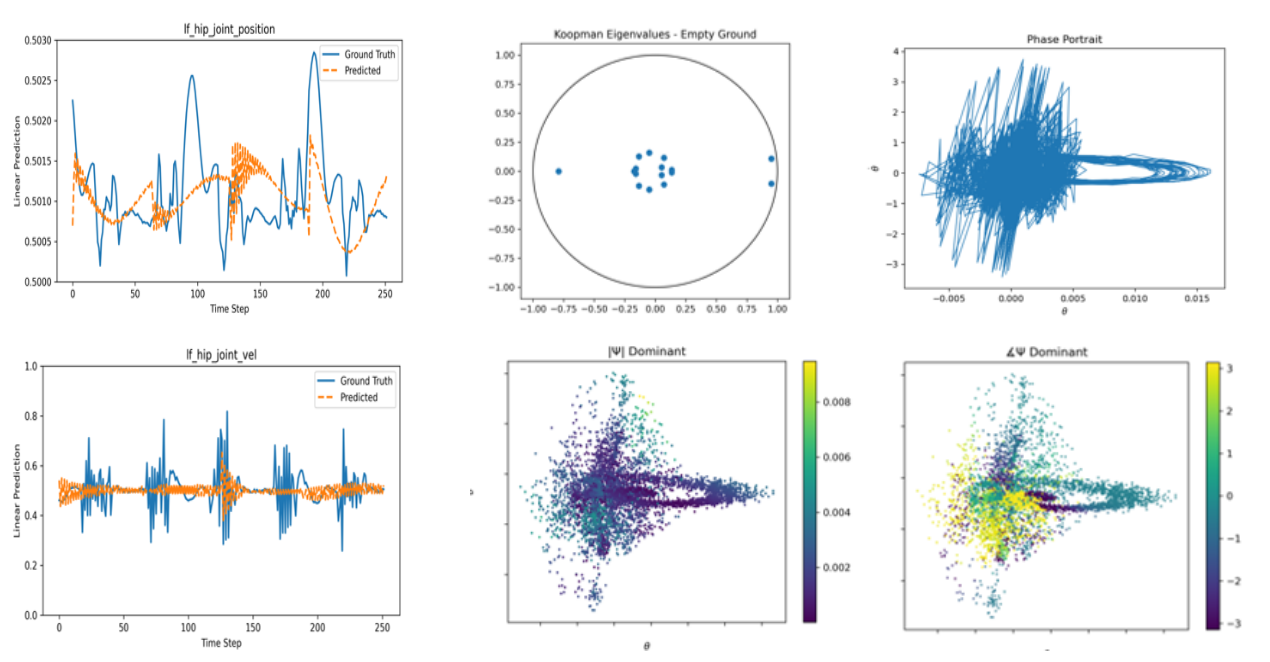
The Koopman Operator theory consists of finding a lifting (i.e. mapping to a infinite, or high in practice, dimensional space) where the dynamics of the system is represented linearly. This is represented by the form:
$[\mathcal{K}g](x_k):=g\circ F(x) = g(x_{k+1})$
where $g$ is the set of observables and $\mathcal{K}$ is the operator propagating the observables forward linearly. Thus, the rich history in linear system analysis and our tools to analyze linear systems can be used. However, finding this lifting is not trivial. By combining the neural network framework, a great function approximation tool, we can negate the daunting task of finding the right lifted space. Note, the demerit to this methodology is that the lifting is a black box and there is not a explicit expression for this lifted space. To have a more in depth understanding of Koopman theory, I recommend Igor Mezic’s Spectrum of the Koopman Operator Theory. For a lighter introduction, I recommend Steve Brunton’s Modern Koopman Theory for Dynamical Systems.
Architecture
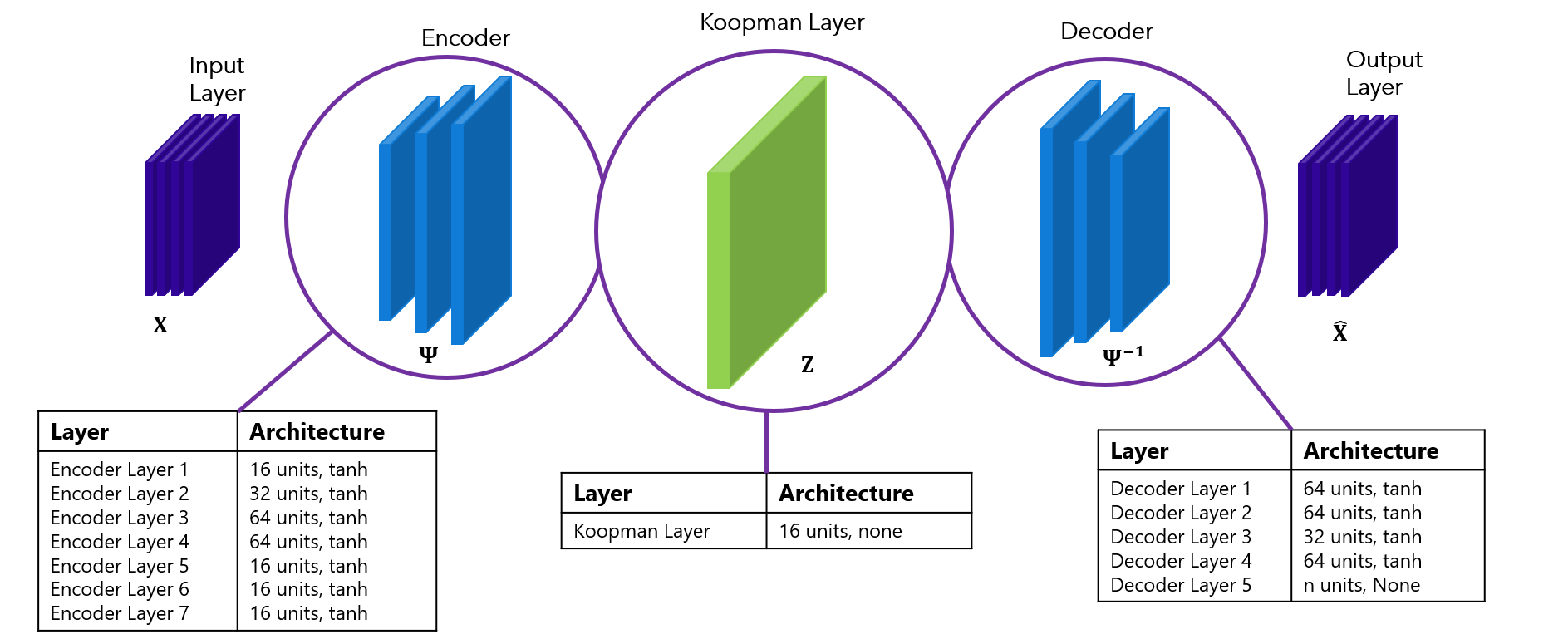
We use an autoencoder as the neural network architecture due to it’s reconstructive capabilities. This allows us to learn the lifting function through data from a specified dynamical system. Moreso, we create a custom autoencoder by incorporating a Koopman Layer , a layer that handles outputting the following states,
$g(x_k), g(x_{k+1}), g(x_{k+i})$.
This allows us to train a autoencoder to incorporate physics-based losses, such as reconstruction loss, dynamical system loss, and linearity loss.
Methodology
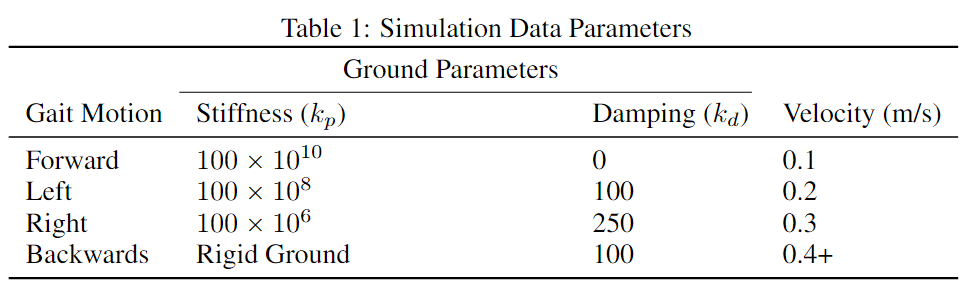
The quadruped locomotion was simulated in gazebo simulation using the champ quadruped model. A automated simulation testbed was generated (can be ran through my github repository) to conduct quadruped locomotion under the following parameters shown in the table below:
By feeding the data collected by the simulation environment into the Koopman autoencoder model, we use the loss terms such as reconstruction error and linearity error to enforce the neural network to learn a dynamical system model.
Results & Conclusion
The graph below shows the results of the Koopman operator, specifically the hip joint position and hip joint velocity. The two left most graph showcases the linearity prediction (prediction for n time steps) using the Koopman autoencoder model. The graph showcases promising results for the high dimensional nonlinear system. The last four remaining graphs showcases the spectrum of the Koopman operator and the values corresponding with the most dominant eigenfunction.