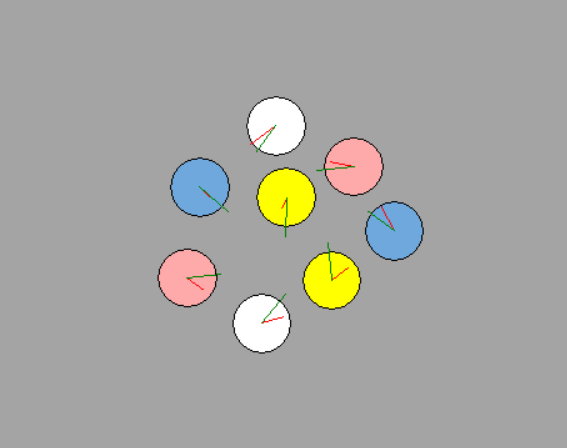
Multiagent Local Navigation
Published:
Multiagent Local Navigation
In this work, I analyze classical multi agent local navigation techniques. The following algorithms were simulated and compared with one another:
- Social Force Model (SFM) (from “Simulating Dynamical Features of Escape Panic” by Dirk Helbing, et. al.)
- Predictive Time to Collision (TTC) Algorithms
- Sampling-based Velocity Obstacles (VO) Algorithm
Review of each Algorithm
We review the nature of each of the algorithm and later compare the algorithm in a multi-agent navigation scenario ranging from 3 or 8 agents.
Social Force Model
The SFM is a reactive based motion planning algorithm in which the crux of the algorithm relies on the attractive force from the goal and the interaction force from neighboring agents/pedestrians (i.e. distance between agents). The authors modeled the interaction force by 3 core components:
- Repulsive interaction force (i.e. force that repels the closer the agent gets to another agent) defined by $F_{repulsive}:=A_i\exp(r_{ij}-d_{ij})/B_i$ where $A_i, B_i$ are some tuning parameters and $r_{ij}$ and $d_{ij}$ are the sum of the radii of the agents and distance between the agents’ center of mass, respectively.
- Body force (i.e. counteracting force in the normal/compression direction when colliding) defined by $F_{body}:=kg(r_{ij}-d_{ij})\bf{n_{ij}}$ where $k$ is some tuning parameter, $\bf{n_{ij}}$ is the normal direction, and g(x) is a switch function that is zero if $d_{ij} > r_{ij}$, otherwise equal to the argument x.
- Sliding friction force (i.e. hinders tangential motion) is defined as $F_{sliding friction}:=\kappa g(r_{ij}-d_{ij})\Delta v_{ji}^t\bf{t_{ij}}$ where $\kappa$ is a scaling parameter, $\Delta v_{ji}^t := (\bf{v}_j- \bf{v}_i) \cdot \bf{t} _{ij}$ is the velocity difference in the tangential direction.
Predictive Time to Collision (TTC) Algorithms
The predictive TTC algorithms relies on a linear velocity assumption for the obstacles/neighboring agents. Base of this assumption and a sensing radius, a time to collision is computed for each neighboring agent’s future position under linear velocity assumption. If the time to collision is finite, a corresponding reactive force is computed based off a scaling parameter. The core predictive avoidance force is defined as such:
$f_{avoid} := \frac{max(\tau_h - \tau, 0)}{\tau}\bf{n}_{AB}$
where $\tau_h$ is the cutoff time to collision horizon, $\tau$ is the time to collision, and $\bf{n_{AB}}$ is the normal direction with respect to the future collision.
Sampling-based VO Algorithm
The sampling-based VO algorithm uses sampling of admissible candidate velocities (i.e. velocity bounds) to find the best control law for the agent. Given the candidate velocities, a cost function is formulated which penalizes the candidate velocities that are within the conic regions representing the velocity obstacles. Moreso, candidate velocities ($\bf{v}^{vcand}$) within the VO region can be represented by the time to collision ($\tau$). Therefore, the best sampled candidate velocity minimizes the following cost function:
$min_{v^{vcand}_i} J = \alpha ||\bf{v}_i^{vcand} - \bf{v}^{goal} || + \beta ||\bf{v}_i^{vcand} - \bf{v} || + \frac{\gamma}{\tau}$
where $\bf{v}^{goal}$ is the goal velocity, $\bf{v}$ is the current velocity, and $\alpha, \beta, \gamma$, are tunable parameters. Therefore, the cost function is a management between penalization of difference in candidate velocity to goal, candidate velocity to current, and candidate velocities within VO’s represented by $\tau$.
Simulation Results
Simulation results for the three algorithms were conducted for scenes with 3 agents passing along a hallways and 8 agents navigating through each other to reach a desired goal position without collision. For each scene, 5 simulations were conducted, 1 for SFM, 2 for predictive TTC (w/ sensory noise $\epsilon$ = 0, 0.2, and sampling-based VO (w/ $\epsilon$ = 0, 0.2).
I list the major tuning parameters for each of the algorithm. Minor parameter details can be looked through within the code.
SFM:
- Sensing radius, $d_{hor} $: 5 [m]
- Relaxation time to compute goal force, $\xi$ : 0.5
- Mass, m: 80 [kg]
- Max force, $F_{max}$: 500 [N]
- Scaling constant for repulsive force, A: 2000
- Safe distance that agent prefer to keep, B: 0.08
- Scaling repulsive force due to collision, k: 1.2e5
- Sliding friction constant due to collision, $\kappa$: 2.4e5
Predictive TTC:
- Sensing radius, $d_{hor}$: 5 [m]
- Relaxation time to compute goal force, $\xi$ : 0.5
- Time horizon, $\tau_h$: 5 [s]
- Sensing noise: $\epsilon$: 0, 0.2
- Mass, m: 1 [kg]
- Max force, $F_{max}$: 10 [N]
Sampling-based VO:
- Sensing radius, $d_{hor}$: 5 [m]
- Tuning parameter to penalize difference in candidate and goal velocity, $\alpha$: 1
- Tuning paramter to penalize difference in candidate and current velocity, $\beta$: 1
- Tuning parameter to penalize collision, $\gamma$: 5
- Sampling number, N: 150
3-agents
The following simulation for the SFM algorithm shows a reactive based force control motion planning algorithm. Although the implementation of this algorithm is the most simple, it is also the most unnatural. The agents only react when close proximity to one another. Moreso, if the agents will not collide with one another, the reactive based control still executes if within a radius. However, for the 3-agent simulation, this reactive force based method is sufficient enough for navigation and obstacle avoidance. Interesting things to note, is that for large relaxation time on goal force ( $\xi$ large), the attractive force of the goal is not as strong. Therefore, when colliding with the obstacles, the agents bounce off due to the repulsive force and slowly heads toward the goal. One drawback of this method is the heuristic formulation of the reactive force methods. It does not guarantee obstacle avoidance and is reliant on tuning parameters.
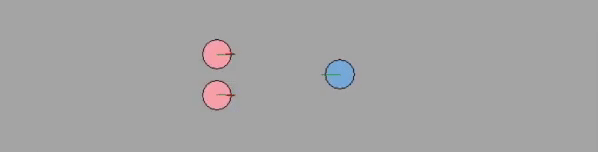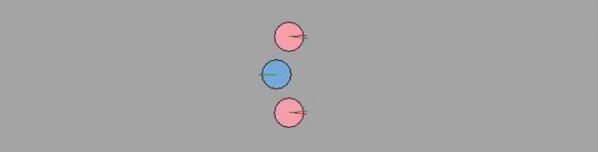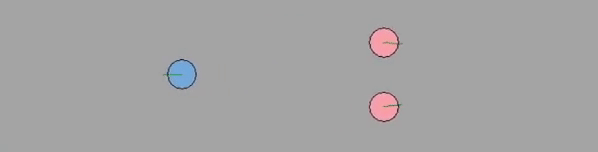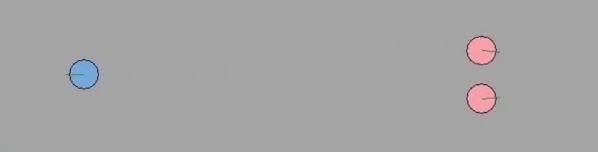
For TTC algorithm, the simulation result is much more natural. The agents reacts apriori if there is a collision course assuming linear velocity of the agent. Therefore, based on the time-to-collision parameter, the agents gradually starts to avoid each other the closer the time there is to collide, which is more similar to human navigation. Although the complexity of the algorithm is slightly more difficult than the reactive based planner (SFM), the results are much better than SFM. While increasing the sensory noise / estimation noise ( $\epsilon = 0 \to 0.2$ ), it is seen that the predictive TTC algorithm makes more conservative actions due to smaller time to collision values from the sensory noise. Similar drawbacks spoken about the SFM algorithm can be stated for the predictive TTC algorithm.

Lastly, for sampling-based VO, the simulation results showcase decent results. As the number of sampling for admissable velocities not within the VO regions increases, the navigation of the single integrator systems collides less and less with the other agents. However, the downside of the results are that the computational complexity increases quadratically. Therefore, although for larger sampling, the likelihood of sampling a candidate velocity that is collision free increase (if it exists), the time to compute a corresponding velocity may not be worth the cost. Additionally, due to the random nature of the sample-based VO, the control taken is not deterministic. Therefore, despite sampling the action for your agent (e.g. velocity), we can get “unlucky” and choose a candidate velocity that heads towards an obstacle even if a feasible velocity that is obstacle free exists. For sensory noise of $\epsilon = 0.2$, the sampling based algorithm choose more conservative candidate velocities as expected. This is due to the fact that the time to collision is more conservative.
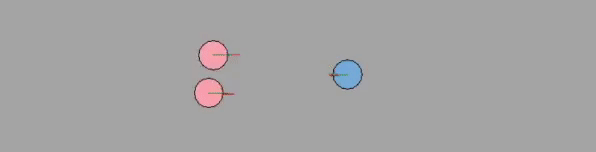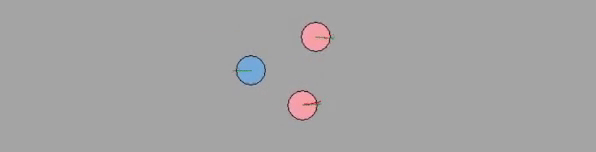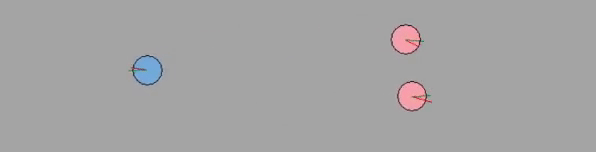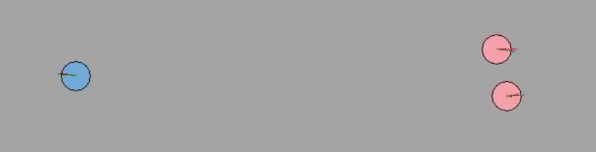
8-agents
The algorithms for an 8-agent simulation is where the algorithms are tested and we truly see the results diverging further. Additionally, this is where the tuning parameters are relied on for better performance. In the 8-agent simulation, all algorithms are more likely to have collisions if not tuned well.
For the SFM algorithm, like previously stated, there is no predictive capabilities. Therefore, the manuever of the agents are purely attractive and then repulsive forces. Thus, the agents collide headstrong and are repulsed later until some asymmetry in the positions breaks the status quo. The agents are somewhat slow to converge to the goal, but nevertheless, the agents reach the goal. However, if there did not exist any asymmetry in this algorithm, there certainly exists questions of local minimas in the navigation problem.
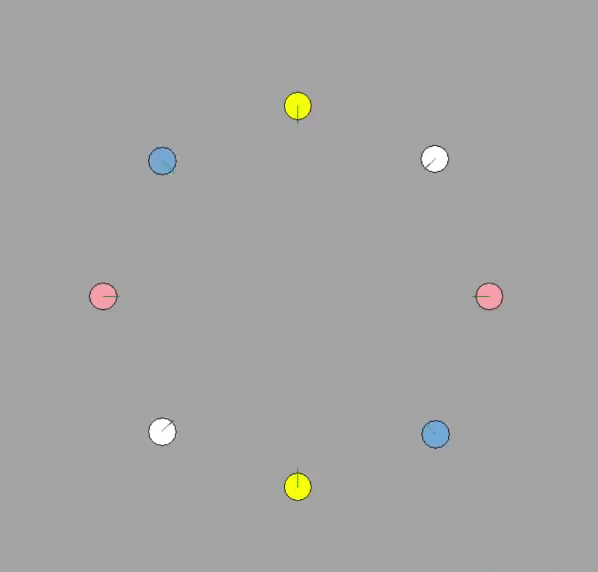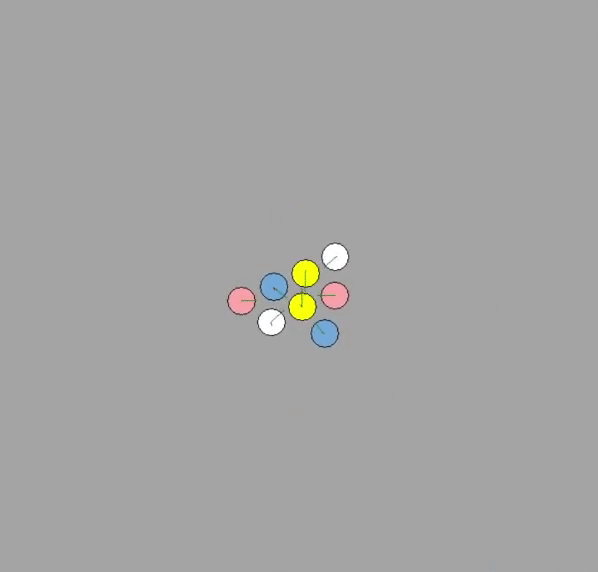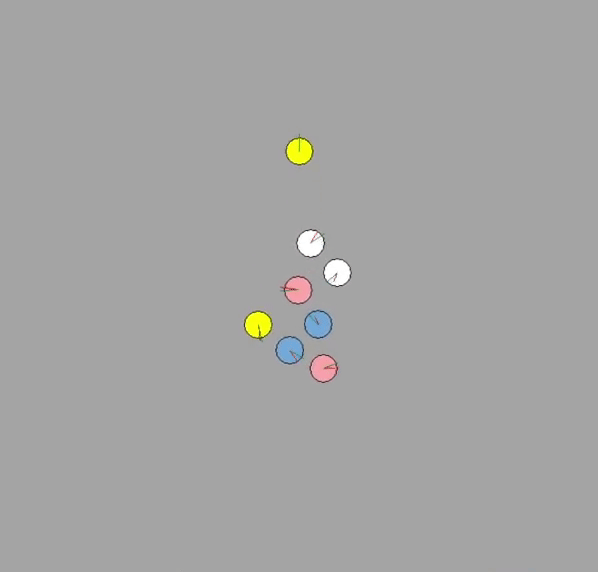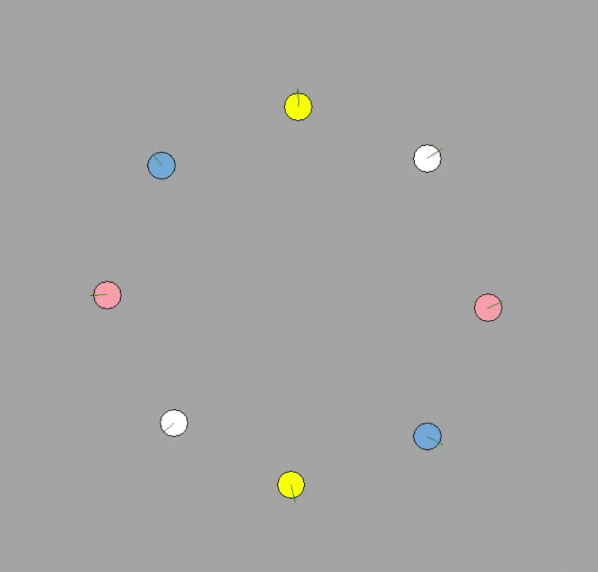
For predictive TTC algorithm, the results are somewhat more interesting. Each of the 8 agents use the predictive capabilities to avoid collision. This gives a somewhat spiral pattern as each agent diverge slightly to a side. The TTC algorithm does not deal with the “stalemate” as long as the SFM algorithm due to predictive capabilties moving the agents before close contact. Similarly, the difference between $\epsilon=0 \to 0.2$ did not see much difference in results. The algorithm simply made more conservative paths. However, if the estimated velocities were to be probablistic, the paths would be fairly different, and incorporating uncertainty in the time-to-collision computation robustifies the noisy data.

Lastly, sample-based VO sees a large variety of results. Due the randomness of each agent and the interaction of these probablistic actions, the simulation runs are fairly unique. The algorithm is capable of generating new solution unlike the other two deterministic algorithms, which gives it a somewhat exploratory behavior. Likewise, given enough sampling (e.g. N = 150), the path taken is typically free from collision. Incorporating $\epsilon = 0, 0.2$ causes the sample-based algorithm to be more conservative, which helps the collision avoidance given that the estimated velocity was noisy.

Conclusion
In conclusion, all three algorithms gives fairly good results for multi agent local navigation. SFM algorithm is by far the easiest to compute and gives fairly decent results in terms of navigation and obstacle avoidance. However, the algorithm is unnatural and have no predictive capabilities, giving it a headstrong path planning characteristic. The predictive TTC algorithm is more natural as it smoothly diverges if another agent/obstacle will collide with the agent itself. The predictive manuever of the agent gives smoother paths, which in practice, most likely helps the system manage the plan better. Lastly, the sample-based VO algorithm gives the most unique paths. It is more exploratory in the path taken. However, this also gives no guarantees for obstacle avoidance for small sampling size. Furthermore, although higher number of sampling increase likelihood of finding feasible obstacle free velocities, there is an increase in computation complexity.
Each algorithm has its general strengths and weaknesses. The preferences of the three algorithm that I would select is the predictive TTC and sample-based VO. Predictive TTC gives smoother trajectories with moderate level of implementations while sample-based VO gives a wider range of feasible solutions but at the cost of computational cost.